Question 1150145: A minivan leaves Topeka at 8:00am. Half an hour later, a car leaves Topeka and follows the same route as the minivan. The car's speed is 5mph faster than the minivan's speed. If the car catches up to the minivan at 3:30 pm, how fast is each vehicle traveling?
Found 2 solutions by ikleyn, josmiceli:
Answer by ikleyn(52864)   (Show Source):
You can put this solution on YOUR website! .
Before the catching moment, the minivan was on the way 7.5 hours, from 8:00 am to 3:30 pm.
The car was on the way half an hour less, i.e. 7.5-0.5 = 7 hours.
Let x be the average speed of the minivan, in miles per hpur.
Then the average speed of the car was (x+5) mph, according to the condition.
To the catching moment, they covered the same distance. Hence,
7.5*x = 7*(x+5).
From this equation,
7.5x = 7x + 35
7.5x - 7x = 35
0.5x = 35
x = 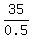 = 70.
ANSWER. The minivan average speed was 70 mph. That of car was 70+5 = 75 mph.
Solved.
Answer by josmiceli(19441)  (Show Source):
|
|
|
