Question 1144208: student tickets at a high school basketball game cost $2.50 each adult tickets cost $6 each the ticket sales at the first game of the season total $7,000 write a model that shows the numbers of student and adult ticket that could have been sold then graph the model and determine three combinations of student and adult tickets that satisfy the model
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52767)   (Show Source):
You can put this solution on YOUR website! .
If x is the number of student tickets and y is the number of adult tickets, then the revenue is 2.50*x + 6*y dollars.
The model, the problem asks for, is this equation
2.50x + 6y = 7000 dollars, (1)
saying that the revenue is 7000 dollars.
Equation (1) represent a straight line y =  .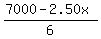
The positive integer numbers x and y satisfying equation (1), represent possible solutions to the problem.
With the only one equation (1), there are many such solutions.
For example, you may check it on your own, that the pairs (x,y) = (4,1165), (16,1160), (28,1155) are integer solutions to equation (1).
With only one restriction (1) to two variables x and y, there are many solutions to this equation.
In typical "ticket problem", in addition to one restriction (1) on revenue, the second restriction on the total number
of items x + y usually comes.
Then with two restrictions for two variables x and y, the problem has a unique solution (if the problem is posed correctly).
Happy learning (!)
On standard ticket problems, see the lessons
- Using systems of equations to solve problems on tickets
- Three methods for solving standard (typical) problems on tickets
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
do you have something against the use of punctuation and capitalization it makes it hard to read your post when everything is just run together it might be okay to write like this when you are texting with your friends but its rather rude when you are asking for help with a problem you certainly wouldn't want to write like this when writing a resume when applying for a job
Please be more polite the next time you post a question to the forum....
Let s = number of students
Let a = number of adults
Then the cost in dollars of s tickets at $2.50 each is 2.5s, and the cost of a tickets at $6 each is 6a. Then since the total ticket sales in dollars was 7000,
There's your "model".
You can draw the graph as easily as I can....
As for finding combinations of student and adult tickets that can make a total of $7000, note that
(1) the cost of each adult ticket is a whole number, so the total cost of the adult tickets is a whole number; and the total ticket sales amount is a whole number. That means the total cost of the student tickets must be a whole number; and that means the number of student tickets must be even. So we can think of the student tickets being sold in pairs, for $5 a pair.
(2) So the total cost of the student tickets is a multiple of $5, and the total ticket sales amount is a multiple of $5; that means the total cost of the adult tickets must be a multiple of $5. At $6 each, that means the number of adult tickets must be a multiple of 5.
So to find combinations of adult and student tickets that will yield the $7000 total, you can choose any numbers of adult tickets that are multiples of 5 and then do some arithmetic to determine the corresponding number of student tickets.
|
|
|
