.
If x is the speed of the plane at no wind (in miles per hour), then
the effective ground speed with the wind is (x+20) mph, while
the effective ground speed against the wind is (x-20) mph.
The "time" equation then is
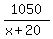 =
= 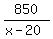 ,
according to the condition (same amount of time for each flight).
To solve it, cross multiply and simplify
1050*(x-20) = 850*(x+20)
1050x - 1050*20 = 850x + 850*20
1050x - 850x = 850*20 + 1050*20
x =
,
according to the condition (same amount of time for each flight).
To solve it, cross multiply and simplify
1050*(x-20) = 850*(x+20)
1050x - 1050*20 = 850x + 850*20
1050x - 850x = 850*20 + 1050*20
x =  = 190.
ANSWER. The speed of the plane at no wind is 190 miles per hour.
CHECK.
= 190.
ANSWER. The speed of the plane at no wind is 190 miles per hour.
CHECK. 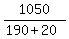 =
= 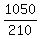 = 5 hours;
= 5 hours; 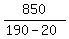 =
=  = 5 hours. ! Correct !
= 5 hours. ! Correct !
Solved.
----------------
The lesson to learn from this solution and the things to memorize are :
1. The effective speed of a plane flying with a wind is the sum of the two speeds.
2. The effective speed of a plane flying against a wind is the difference of the two speeds.
3. It gives you a "time" equation, which you easily can solve and find the unknown plane' speed.