Question 1134548: In a two-mile race, Ed can beat Faith by 1/5 of a mile. In a two-mile race,
Faith can beat Matt by 1/10 of a mile. If Ed and Matt were to have a two mile race, by how much would Ed win?
Found 2 solutions by ankor@dixie-net.com, ikleyn:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a two-mile race, Ed can beat Faith by 1/5 of a mile.
In a two-mile race, Faith can beat Matt by 1/10 of a mile.
If Ed and Matt were to have a two mile race, by how much would Ed win?
:
Change 1/5 mi to .2 mi
:
Ed goes 2 mi
while
Faith goes (2-.2) = 1.8mi
and
Math goes (2-.2-.1) = 1.7 mi
:
Ed would win over Mat by 2 - 1.7 = .3 mi
:
It Pains me to say it, but ikleyn is absolutely right! I thought it over as I retired last night and realized it. If they all raced at the same time, it would have been OK, but obviously they did not. I am truly sorry for misleading you. CK
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution by the tutor @ankor@dixie-net.com is WRONG.
What is even worst, it is CONCEPTUALLY wrong, which means that the idea of the solution is wrong.
The right solution should use the conceptions of velocities (rates) and rate ratios.
See my solution below.
Let  be the Ed's rate, in miles per hour; be the Ed's rate, in miles per hour;
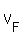 be the Faith's rate, and be the Faith's rate, and
 be the Matt rate.
Since in a two-mile race, Ed can beat Faith by be the Matt rate.
Since in a two-mile race, Ed can beat Faith by  = 0.2 of a mile, it means that the ratio of their rates is = 0.2 of a mile, it means that the ratio of their rates is  = =  = =  .
It is totally clear: in that time as Ed will complete the 2 miles race, Faith will cover only 2-0.2 = 1.8 miles.
Next, since in a two-mile race, Faith can beat Math by .
It is totally clear: in that time as Ed will complete the 2 miles race, Faith will cover only 2-0.2 = 1.8 miles.
Next, since in a two-mile race, Faith can beat Math by 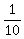 = 0.1 of a mile, it means that the ratio of their rates is = 0.1 of a mile, it means that the ratio of their rates is  = =  = =  .
It implies that the ratio of the rates .
It implies that the ratio of the rates  = = 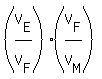 = =  = =  = =  = =  .
It means that in the 2 miles race Ed can beat Matt by 2 - 1.71 = 0.29 miles. ANSWER .
It means that in the 2 miles race Ed can beat Matt by 2 - 1.71 = 0.29 miles. ANSWER
Solved.
|
|
|