SOLUTION: Alonzos boat has a top speed of 20 miles per hour in still water. While traveling on a river at top speed, he went 40 miles upstream in the same amount of time he went 60 miles dow

Let x = the rate of the river current, in miles per hour.


Then the effective rate downstream is  (20+x) mph, 
while the effective rate upstream  is  (20-x) mph.


The time traveling 40 miles upstream   is  .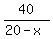

The time traveling 60 miles downstream is  .


The times are equal, so you have an equation


     = .


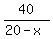To solve it, multiply both sides by  20-x)*(20+x). You will get


    40*(20+x) = 60*(20-x),

    800 + 40x = 1200 - 60x

    40x + 60x = 1200 - 800

    100x = 400   ======>  x = 400/100 = 4.


Answer.  The rate of the river current is 4 miles per hour.