Question 1112429: what is the reference angle for a 960 degree angle? show all work please
Found 2 solutions by Theo, KMST:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! first you find the equivalent positive angle between 0 and 360 degrees.
just subtract 360 from 960 until you get there.
960 - 360 = 600 - 360 = 240
the equivalent angle between 0 and 360 degrees is 240 degrees.
that angle is in the third quadrant.
the reference angle for an angle in the third quadrant is that angle minus 180 degrees.
240 - 180 = 60 degrees.
that's your reference angle.
you can use your calculator to confirm.
if the angle is the reference angle, then the sine and cosine and tangent of the angle will be the same as the sine and cosine and tangent of the reference angle except for the sign.
the sine in the third quadrant is negative.
the cosine in the third quadrant is negative.
the tangent in the third quadrant is positive.
using my calculator, i get:
sin(60) = + .8660254038
cos(60) = + .5
tan(60) = + 1.732050808
sin(240) = - .8660254038
cos(240) = - .5
tan(240) = + 1.732050808
the trig functions are the same except for the sign, therefore 60 degrees is the reference angle for 240 degrees.
to confirm that 240 degrees is equivalent to 960 degrees, i got the trig functions for 960 degrees, using my calculator.
sin(960) = - .8660254038
cos(960) = - .5
tan(960) = + 1.732050808
that's identical to the trig functions for 240 degrees, therefore 960 degrees and 240 degrees are equivalent.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is what a 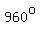 looks like, looks like,
 It's 2 turns and It's 2 turns and 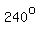 (all counterclockwise, of course). (all counterclockwise, of course).
When you divide 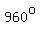 by by  the quotient is the quotient is  and the remainder is and the remainder is 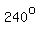 . .
You do not need to divide (unless the angle measure is huge).
You can keep subtracting  (one turn) until you get less than one turn. (one turn) until you get less than one turn.
You can write that as
 , or , or  , or , or  . .
Now you have to work with 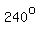 , the co-terminal angle of , the co-terminal angle of 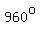 . .
An angle measuring 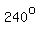 is in the third quadrant, is in the third quadrant,
where all the angles between  and and 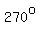 are located. are located.
You can write that as
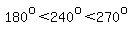 . .
The reference angle is a symmetrical angle in quadrant I, and that angle has the same absolute value for all trigonometric functions.
For quadrant III, it is easy, you just subtract half a turn<,  , ,
and that gives you the angle with the opposite ray for a terminal side:
 The reference angle is The reference angle is  . .
|
|
|