Question 1103620: An aircraft flew 4 hours with the wind. The return trip took 5 hours against the wind. If the speed of the plane in still air is 184 miles per hour more than the speed of the wind, find the wind speed and the speed of the plane in still air.
Found 2 solutions by ikleyn, richwmiller:
Answer by ikleyn(52746)   (Show Source):
You can put this solution on YOUR website! .
An aircraft flew 4 hours with the wind. The return trip took 5 hours against the wind. If the speed of the plane in still air
is 184 miles per hour more than the speed of the wind, find the wind speed and the speed of the plane in still air.
~~~~~~~~~~~~~~~~~~~~~~~~~
In such/(in similar) problems the term "in still water" is commonly accepted;
but the term "in still air" is NEVER used.
Instead, the term "at no wind" is used.
Let "u" be the aircraft speed at no wind (in miles per hour), and
let "v" be speed of the wind.
Then the aircraft tailwind speed is (u+v) mph,
while the aircraft speed against the wind is (u-v) mph, which is exactly 184 mph.
Therefore, the one-way distance aircraft covered flying against the wind was
184*5 = 920 miles.
Hence, flying tailwind, the aircraft tailwind speed was u+v = 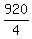 = 230 mph.
Now you have these two equations
u + v = 230, (1)
u - v = 184. (2) (given).
----------------------------------------Add the equations (both sides). You will get
2u = 230 + 184 = 414 ====> u = 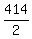 = 207.
Then from eq(1), v = 230 - 207 = 23.
Answer. The aircraft speed at no wind is 207 mph. The speed of the wind is 23 mph.
---------------------
It is a typical "tailwind and headwind" word problem.
See the lessons
- Wind and Current problems
- Wind and Current problems solvable by quadratic equations
- Selected problems from the archive on a plane flying with and against the wind
in this site.
In these lessons you will find the detailed solutions of many similar problems.
Consider them as samples. Read them attentively.
In this way you will learn how to solve similar problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by richwmiller(17219)  (Show Source):
You can put this solution on YOUR website! As a native English speaker and former English teacher, I can say that the phrase "in still air" is acceptable and actually preferred. The phrase "at no wind" is awkward. The phrase "with no wind" could also be used.
r=w+184
r*t=d
With the wind
(r+w)*t=d
(r+w)*4=d
r=w+184
(w+184+w)*4=d
(2w+184)*4=d
8w+736=d
r=w+184
Against the wind
(r-w)*t=d
r=w+184
(w+184-w)*5=d
184*5=d
920=d distance
8w+736=920
8w=184
w=184/8
w=23 mph wind speed
r=w+184
r=23+184
r=207 mph plane speed in still air or with no wind
check
(207+23)*4= (207-23)*5
230*4=184*5
920=920
ok
|
|
|
