SOLUTION: Assume 365 days per year. If 15 people are selected at random, what is the probability that at least two of them will have the same birthday?

Let us consider how many situations are possible when all 15 people have their birthdays in different days and 
       there are no two whose birthdays coincide.


The number of such cases is equal to 

P = 365*364*363* . . . *(365-15+1) = 365*364*363* . . . *351 = 2.03129E+38    (integer number).


The whole space of events contains 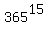  = 2.7189E+38  elements.


Hence, the probability under the question is  1 -  = 0.253.