Question 1071978: A motor boat took 5 hours to travel 24km down the river to another town and to return. At another time the boat took 4 hours to travel 12km downstream and 24km upstream. Find the speed of the boat in still water and the speed of the river
Answer by ikleyn(52785)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A motor boat took 5 hours to travel 24km down the river to another town and to return. At another time the boat took
4 hours to travel 12km downstream and 24km upstream. Find the speed of the boat in still water and the speed of the river
~~~~~~~~~~~~~~~~~~~~~~~~~~
Let "u" be the motorboat speed in still water, in mph, and
Let "v" be the current rate.
Then the motorboat effective speed downstream is (u+v) mph, while upstream (u-v) mph.
The governing equations are
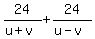 = 5, (1) = 5, (1)
 = 4. (2)
To solve the system (1),(2), subtract (2) from (1). You will get = 4. (2)
To solve the system (1),(2), subtract (2) from (1). You will get
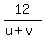 = 1 ====> u + v = 12. (3)
Having this, from (1) you get = 1 ====> u + v = 12. (3)
Having this, from (1) you get
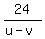 = = 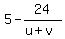 = 5 - 2 = 3. Hence, u - v = = 5 - 2 = 3. Hence, u - v =  = 8. (4)
Again,
u + v = 12, (3)
u - v = 8. (4)
Add (3) and (4). You will get
2u = 12 + 8 = 20. Hence, u = 10.
Then from (3) v = 12 - 10 = 2.
Answer. The motorboat speed in still water is 10 mph. The current speed is 2 mph. = 8. (4)
Again,
u + v = 12, (3)
u - v = 8. (4)
Add (3) and (4). You will get
2u = 12 + 8 = 20. Hence, u = 10.
Then from (3) v = 12 - 10 = 2.
Answer. The motorboat speed in still water is 10 mph. The current speed is 2 mph.
Solved.
For many similar problems see the lessons
- Wind and Current problems
- More problems on upstream and downstream round trips
- Wind and Current problems solvable by quadratic equations
- Unpowered raft floating downstream along a river
- Selected problems from the archive on the boat floating Upstream and Downstream
- Selected problems from the archive on a plane flying with and against the wind
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Travel and distance".
|
|
|