Question 1068621: A ball is thrown vertically upward. After t seconds, its height h (in feet) is given by the function
h(t) = 60t - 16t^2
What is the maximum height that the ball will reach?
Do not round your answer.
Height: _____ feet
Please show steps to answer this problem. Thank you.
Found 3 solutions by KMST, ikleyn, josgarithmetic:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The function  , which could be written as  ,
is a quadratic function
(a polynomial with degree 2),
and graphs as a parabola.
Your teacher probably wants to remember all the names and formulas.
WITH FORMULAS:
You have probably studied quadratic functions of the form
 and were told that they have
a maximum if  , or a minimum is 
at  .
That point in the graph is also called the vertex of the parabola.
In this case, the variable is called  instead of  ,
and the coefficients are
 ,  , and  .
So the maximum happens at 
So the maximum is
 .
WITH EASE (AND THINKING):
Those parabolas are symmetrical,
so if a parabola has two zeros,
the maximum or minimum happens halfway between the zeros.
This parabola must have two zeros
and a maximum in between because the ball
was thrown up from the ground (how did they do that?)
gets to some maximum height,
and falls back to the ground on the ground.
Let me find the zeros by factoring.
So, the zeros are  and
(from  <--> <--> )  .
The maximum happens halfway between and .
So, it happens at  .
The maximum is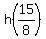 
 .
Either way, the maximum height is  .
Answer by ikleyn(52784)  (Show Source):
Answer by josgarithmetic(39617)  (Show Source):
|
|
|
