Question 1067677: A truck enters a highway driving 60 mph. A car enters the highway at the same place 5 minutes later and drives 68 mph in the same direction. From the time the car enters the highway, how long will it take the car to pass the truck?
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! When the car enters the highway, the truck has gone 5 miles.
The question is how long does it take a car going 8 mph faster than a truck to travel a mile, and that is 5/8 of an hour or 37.5 minutes.
Algebraically, one can do this by saying the car will catch the truck in x minutes, using minutes here, because the truck is conveniently going a mile a minute.
during that time, the truck will have gone 5+x miles in 5+x minutes.
the car is going at 68 mph (1.13333 miles/minute) and passes the truck in x minutes.
When they are even, the truck has travelled 5+x miles and the car 1.1333333x miles
Setting those equal, since they are, the 5=0.13333333x
and x=37.50 minutes.
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let t be the time under the question, in hours.
Then the truck traveled the distance 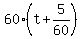 = 60t + 5 miles before the car passed the truck.
The car traveled the distance 68*t.
The distances are the same, which gives you an equation
60t + 5 = 68t ---> 68t - 60t = 5 ---> 8t = 5, t = = 60t + 5 miles before the car passed the truck.
The car traveled the distance 68*t.
The distances are the same, which gives you an equation
60t + 5 = 68t ---> 68t - 60t = 5 ---> 8t = 5, t = 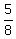 of an hour = 37 minutes 30 seconds. of an hour = 37 minutes 30 seconds.
|
|
|