SOLUTION: A tour bus averaged 50 miles per hour between two cities on the first leg of a trip and 45 miles per hour on the return trip. The return trip took 1/2 hour longer. Find the distanc

                    RATE             TIME          DISTANCE

ONE WAY             50                t             d

OTHER WAY           45               t+1/2          d

g for the rate GOING and r for the rate RETURNING;
Unknown variables are t and d.



                    RATE             TIME          DISTANCE

ONE WAY             g                t              d

OTHER WAY           r               t+h             d

Let "t" be the time spent on the first leg at the average speed of 50 miles per hour.

Then (t+0.5) is the time spent on the returning trip at the average speed of 45 miles per hour.
   (Here o.5 is 1/2 of an hour)

Since the distance is the same in both directions, you have an equation

50*t = 45*(t+0.5).

Simplify and solve it for "t".

50t = 45t + 22.5,

5t = 22.5  --->  t =  = 4.5.

Thus we found the time spent at the speed 50 mph. It is 4.5 hours.
Then the distance between the cities is 50*4.5 = 225 miles.

Check. The returning trip takes 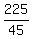 = 5 hours, which is 1/2 hour  longer than 4.5 hours.  The solution is checked and is correct.

Answer.   The distance between the cities is 50*4.5 = 225 miles.

Let D be the distance between the cities. Then the condition directly says that

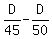 = 0.5.

The first term in the left side is the time spent on the returning trip.
The second term in the left is the time spent on the first leg trip.
The difference of the terms on the left is that 0.5 hour.

Multiply both sides of the equation by 450. You will get

10D - 9D = 225, or

D = 225.

You got the same answer for the distance.

Congratulations !