Lesson Miles per gallon effectiveness and moving car

Miles per gallon effectiveness and moving car

Problem 1

Let x be the number of gallons were consumed by the first car.

Then the number of gallons consumed by the second car is  (45-x).


The distance traveled by the first car is 40x miles.

The distance traveled by the second car is 25*(45-x) miles.


The total distance equation is

    40x + 25*(45-x) = 1575  miles.


From this equation, express x and calculate

    x = 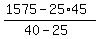 = 30.


ANSWER.  The first car consumed 30 gallons of fuel.  The second car consumed the rest (45-30) = 15 gallons.

Problem 2

Let x be the distance driven in the city, in miles, and

Then the distance driven on the highway is 465-x miles.


The amount of gasoline spent in the city    is   gallons.

The amount of gasoline spent on the highway is   gallons.


Then the equation for the gasoline spent is


 +  = 18.4.

-

To solve it, multiply left and right sides by 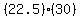 = 12420

7.5x = 12420-10462.5  ====>  x =261.


Answer.  In the city:  261 miles;  on Highway:  204 miles.

Problem 3

Let "h" be the gallons oh highway;  let "c" be the gallons in the city.


Then, from the problem description, you have these two equations for your unknowns

       h +    c =   900       (1)   (total gallons spent last year)

    40*h + 25*c = 30000       (2)   (total distance, in miles, traveled last year)


Your intermediate goal is to find h, the gallons on highway.


From equation (1), express  c = 900-h  and substitute it for c in equation (2).
You will get then

    40h + 25(900-h) = 30000.


Thus you have single equation for your unknown h.
Simplify and find h

    40h + 25*900 - 25h = 30000,

    40h + 25*900 - 25c = 30000,

     40h - 25h = 30000 - 25*900

         15h   =    7500

           h   =    7500/15 = 500.


Thus we found that last year Theresa was allowed 500 gallons on highway.


Hence, the allowed distance on highway was 40*500 miles, or 20,000 miles.


At this point, the problem is solved in full.


ANSWER.  Theresa was allowed 20,000 miles on highway for business expenses last year.

    In this solution, two equations in two unknowns are used.

    But the problem can be solved similarly, using one unknown h, too.

    Using only one unknown for the highway gallons h, the setup equation is

          40h + 25(900-h) = 30000  miles.


     You can solve it then by the same way as it is solved in the solution above.


     I presented here the solution with two unknown only to make your understanding easier.