SOLUTION: When a two-digit number is divided by the product of the two digits, the answer is 2 and if 27 is added to the number, the original number turns into a new number with the digits

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: When a two-digit number is divided by the product of the two digits, the answer is 2 and if 27 is added to the number, the original number turns into a new number with the digits       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 990263: When a two-digit number is divided by the product of the two digits, the answer is 2 and if 27 is added to the number, the original number turns into a new number with the digits being swapped around. Find the number.
Answer by ikleyn(52908) About Me  (Show Source):
You can put this solution on YOUR website!
.
Answer. 36.

Solution

Let  a  and  b  be the first  (the left)  and the second  (the right)  digit of the number respectively,  so that the number is  10a + b.

The first condition says that 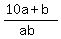 %2810a+%2B+b%29%2F%28ab%29 = 2,   or

10a + b = 2ab.         (1)

The number with swapped digits is  10b + a, so the second condition says that

10a + b + 27 = 10b + a,   or   9a - 9b = -27,   or   a-b = -3.

So,  we have a system of two equations

system%2810a+%2B+b+=+2ab%2C%0D%0Aa-b+=+-3%29.

Express  b  from the last equation,  b = a + 3,  and substitute it into the previous equation.  You will get

10a + a + 3 = 2a*(a+3),   or

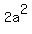2a%5E2 - 5a - 3 = 0.

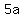Solve this quadratic equation using the quadratic formula.  You will get the roots  a%5B1%5D = 3  and  a%5B2%5D = -1%2F2.
The negative root doesn't suit,  because we are looking for the digit,  which should be non-negative integer less than 10.  The root  a%5B1%5D = 3  is good.

So,  the number is  36.

Please check yourself that this number satisfies all conditions of the problem.