SOLUTION: ind two numbers whose sum is 14 such that the sum of their squares is a minimum. (If a solution has a multiplicity of two, enter it in consecutive answer boxes.) (smaller value)

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: ind two numbers whose sum is 14 such that the sum of their squares is a minimum. (If a solution has a multiplicity of two, enter it in consecutive answer boxes.) (smaller value)      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 942754: ind two numbers whose sum is 14 such that the sum of their squares is a minimum. (If a solution has a multiplicity of two, enter it in consecutive answer boxes.)
(smaller value)
(larger value)
Need Help? Read It Practice It

Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
x^2+y^2=f(something), naming a function.
and
x+y=14

y=14-x
-
f%28x%29=x%5E2%2B%2814-x%29%5E2
f%28x%29=x%5E2%2B196-28x%2Bx%5E2
f%28x%29=2x%5E2-28x%2B196
f%28x%29=2%28x%5E2-14x%2B98%29

The minimum of f is the vertex, and just the quadratic factor part is needed for this. Factorable?

98=2*59, maybe not factorable.

Completing the Square to put into standard form,
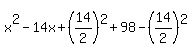
x%5E2-14x%2B%2814%2F2%29%5E2%2B98-%2814%2F2%29%5E2
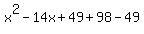
x%5E2-14x%2B49%2B98-49
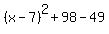
%28x-7%29%5E2%2B98-49
%28x-7%29%5E2%2B49

The vertex, a minimum point, is (7, 49).
The value for x is 7, so this means, according to the given description, y is also 7.