|
Question 914979: true or false
the last line of synthetic division for (2x^4 - 5x^3 + 7x^2 - 3x +1)/(x - 3) gives coefficients for the quotient of 2,1,8, and 21?
Found 2 solutions by ewatrrr, Edwin McCravy:
Answer by ewatrrr(24785)   (Show Source):
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website!
The other tutor made a mistake.
We'll see what it should be. But first of all you should not write
2x^4 - 5x^3 + 7x^2 - 3x +1/ x - 3
because you must indicate with parentheses where every numerator
and denominator begins and ends. You use a "{" to show where they
begin and a ")" to show where they end. IOW, you should have
(2x^4 - 5x^3 + 7x^2 - 3x +1)/(x - 3)
Without the parentheses the only things divided are the 1 and the x.
So in the future be sure to use parentheses to show where numerators
and denominators begin and end.
3 | 2 -5 7 -3 1
| 6 3 30 81
2 1 10 27 82
No, it's 2,1,10,27, and 82. The answer to the division is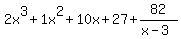 
Edwin
|
|
|
| |
