SOLUTION: find the smallest 7 digit mumber formed by 0,1,2,3 and 5 completely divisible by 198?

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: find the smallest 7 digit mumber formed by 0,1,2,3 and 5 completely divisible by 198?       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 874953: find the smallest 7 digit mumber formed by 0,1,2,3 and 5 completely divisible by 198?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The way I understand the problem,
all the digits listed are required (they have to be in the number),
and no other digits are allowed.

198=2%2A9%2A11 so the number must be a multiple of 2 , 9 and 11.

Including only allowed digits, to be a multiple of 2 ,
the number must end in 2 or %220%22 .

To be a multiple of 9 the number's digits must add to a multiple of 9 .
Since the required digits add up to 0%2B1%2B2%2B3%2B5=11 ,
the sum of all digits cannot add to 9 .
With two more digits the only other multiple of 9 possible for that sum is
2%2A9=18 .
The two extra digits must add to 18-11=7 , so they must be
highlight%282%29 and highlight%285%29 .
So, the seven digits are
highlight%28%220%22%29 , highlight%281%29 , highlight%282%29 , highlight%282%29 , highlight%283%29 , highlight%285%29 , and highlight%285%29 .

For a 7 digit number to be a multiple of 11 ,
the sum of the 1st, 3rd, 5th, and 7th digits, 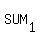SUM%5B1%5D ,
and the sum of the 2nd, 4th, and 6th digits, 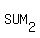SUM%5B2%5D ,
must differ by %220%22 or a multiple of 11 .
In this case, since both sums add to 18 ,
the difference could only be %220%22 or 11 ,
not 22 or other multiples.
So, while we know that SUM%5B1%5D%2BSUM%5B2%5D=18 ,
the sums must also satisfy
SUM%5B1%5D-SUM%5B2%5D=0 or SUM%5B1%5D-SUM%5B2%5D=11 or SUM%5B2%5D%2BSUM%5B1%5D=11 .
Since the systems formed by SUM%5B1%5D-SUM%5B2%5D=11 or SUM%5B2%5D%2BSUM%5B1%5D=11 ,
along with SUM%5B1%5D%2BSUM%5B2%5D=18 , do not have integer results,
the system we have to solve is
system%28SUM%5B1%5D%2BSUM%5B2%5D=18%2CSUM%5B1%5D-SUM%5B2%5D=0%29 .
Its solution is highlight%28system%28SUM%5B1%5D=9%2CSUM%5B2%5D=9%29%29 .
We need to separate the digits to be used,
highlight%28%220%22%29 , highlight%281%29 , highlight%282%29 , highlight%282%29 , highlight%283%29 , highlight%285%29 , and highlight%285%29 ,
into two groups:
a group of 4 digits that add up to SUM%5B1%5D=9 ,
and a group of 3 digits that add up to SUM%5B2%5D=9 .
With those digits, the only ways to get a group of 3 digits that add up to 9 is
highlight%282%2B2%2B5=9%29 or highlight%281%2B3%2B5=9%29 .
One of those groups of digits will include highlight%282%29 , highlight%282%29 , and highlight%285%29 ,
and the other group will include highlight%281%29 , highlight%283%29 , and highlight%285%29 .
The required highlight%28%220%22%29 will have to be added to one of those groups to get the group of 4 digits that will be the 1st, 3rd, 5th, and 7th digits.

To get the smallest possible number, we would want the first digit to be 1 ,
so the 1st, 3rd, 5th, and 7th digits must include
highlight%281%29 , highlight%283%29 , highlight%285%29 , and highlight%28%220%22%29 .
We are choosing highlight%281%29 as the 1st digit.
We need to use highlight%28%220%22%29 as the 7th and last digit,
because the number must be a multiple of 2 .
Regarding the 3rd, and 5th digits, the number will be smallest if
highlight%283%29 is the 3rd digit,
and highlight%285%29 is the 5th digit.
So the 1st, 3rd, 5th, and 7th digits are
highlight%281%29 , highlight%283%29 , highlight%285%29 , and highlight%28%220%22%29 , in that order.

Regarding the 2nd, 4th, and 6th digits, which must include
highlight%282%29 , highlight%282%29 , and highlight%285%29 ,
we get the smallest number if we use them in that order.

So, the number is highlight%281232550%29 .