|
Question 835353: The sum of two numbers is 25.their difference is 7.find the numbers.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! USING JUST ONE VARIABLE:
 = the smaller number = the smaller number
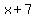 = the larger number (since the difference between them is 7) = the larger number (since the difference between them is 7)
 is our equation (because the sum of the two numbers is 25). is our equation (because the sum of the two numbers is 25).
Solving:






 is the smaller number. is the smaller number.
Then,  is the larger number. is the larger number.
The two numbers are  and and  . .
USING TWO VARIABLES:
 = the smaller number = the smaller number
 = the larger number = the larger number
The equations are
 (because the sum of the two numbers is 25), and (because the sum of the two numbers is 25), and
 (because the difference of the two numbers is 7). (because the difference of the two numbers is 7).
We can solve the system  by substitution by solving by substitution by solving
 for for  , getting , getting  and then substituting and then substituting 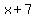 for for  in in  . .
Then we get the one variable equation solved above.
We can also solve the system  by graphing, or by the "method" that some call elimination. (Others call it combinations of equations. by graphing, or by the "method" that some call elimination. (Others call it combinations of equations.
For example, adding both equations, we get


------------
 --> -->  --> -->  ---> h ---> h
Then we can substitute that value for  into either of the equations to find into either of the equations to find  , as in , as in
 --> -->  --> -->  --> -->  . .
To solve by graphing we graph the line that represents  and the line that represents and the line that represents  . The coordinates of the point where they intersect is the (x,y) solution . We estimate it (read it) from the graph, to get the values of x and y that appear to be the solution, and then verify by plugging those values into the equations. . The coordinates of the point where they intersect is the (x,y) solution . We estimate it (read it) from the graph, to get the values of x and y that appear to be the solution, and then verify by plugging those values into the equations.
Graphing is a bit time consuming.
To graph one linear equation, we just need to points (or a pont and a slope).
For  , we can see that (0,25) and {25,0) are two points in the graph, because when we set x to zero, the equation turns into , we can see that (0,25) and {25,0) are two points in the graph, because when we set x to zero, the equation turns into  , and hen we set y to zero, the equation turns into , and hen we set y to zero, the equation turns into  . The points (0,25) and (25,0) are the y-intercept and x-intercept, and we can use them to draw the line. . The points (0,25) and (25,0) are the y-intercept and x-intercept, and we can use them to draw the line.
For  we can find the points (0,7) and (-7,0) in a similar way. we can find the points (0,7) and (-7,0) in a similar way.
 The intersection point coordinates appear to be The intersection point coordinates appear to be  and and  . .
We verify by substituting into  to get to get
 . .
We also need to verify that Those values make  true, so we calculate true, so we calculate
 . .
With the values read from the graph verified, we can say that the solution found by graphing is
 . .
|
|
|
| |