|
Question 823053: While adding the first few continuous natural numbers, a candidate missed one of the numbers and wrote the answer as 177. What was the number missed?
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! While adding the first few continuous natural numbers, a candidate missed one of the numbers and wrote the answer as 177. What was the number missed?
The formula for the sum of the first n natural numbers is 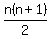 Let the number missed be = k
Let the number missed be = k
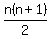 -k = 177 -k = 177
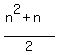 -k = 177
Multiply both sides by 2
nē + n - 2k = 354
nē + n - 354 = 2k
k ≧ 1, so 2k ≧ 2
nē + n - 354 ≧ 2
nē + n - 352 ≧ 0
By the quadratic formula, that has critical
numbers approximately 18.3 and -19.3
In integers the inequality has solutions
n = -20,-21,-23,... and n = 19, 20, 21,...
Since n is positive we take the first integer
value exceeding 18.3, which is 19:
Substituting n=19 in -k = 177
Multiply both sides by 2
nē + n - 2k = 354
nē + n - 354 = 2k
k ≧ 1, so 2k ≧ 2
nē + n - 354 ≧ 2
nē + n - 352 ≧ 0
By the quadratic formula, that has critical
numbers approximately 18.3 and -19.3
In integers the inequality has solutions
n = -20,-21,-23,... and n = 19, 20, 21,...
Since n is positive we take the first integer
value exceeding 18.3, which is 19:
Substituting n=19 in
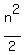 + +  - 177 = k - 177 = k
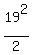 + + 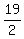 - 177 = k
180.5 + 9.5 - 177 = k
13 = k
Answer: the candidate added the integers 1 through 19, but omitted 13.
-------------------------------------------------
Checking:
So since n = 19, the candidate added this with 13 omitted:
1+2+3+4+5+6+7+8+9+10+11+12+14+15+16+17+18+19 = 177
That checks.
Edwin - 177 = k
180.5 + 9.5 - 177 = k
13 = k
Answer: the candidate added the integers 1 through 19, but omitted 13.
-------------------------------------------------
Checking:
So since n = 19, the candidate added this with 13 omitted:
1+2+3+4+5+6+7+8+9+10+11+12+14+15+16+17+18+19 = 177
That checks.
Edwin
|
|
|
| |