SOLUTION: 25 women did 1/5 of job in 8 days. Then, because of an emergency, it became necessary to complete the job in the next 20 days. How many additional women needed to be added to the c

I'll show you two ways to do this:

25 women can do 1/5 of the job in 8 days. Therefore, 
25 women can do the whole job in 40 days. Therefore,
50 women can do the whole job in 20 days. Therefore,
since only 4/5th of the job needs completing, it will
only take 4/5ths of 50 women to do the remaining 4/5ths
of the job, and 4/5ths of 50 is 40.  They already have
25 women, so they'll need 40-25 or 15 more women. 


Another way to do this is with the worker-time-job formula, which is:



where

W1 = the number of workers in the first situation.
T1 = the number of time units (days in this case) in the first situation.
J1 = the number of jobs (or fraction thereof) in the first situation.

W2 = the number of workers in the second situation.
T2 = the number of time units (days in this case) in the second situation.
J2 = the number of jobs (or fractionthereof) in the second situation.

W1 = 25             W2 = the unknown quantity     
T1 =  8             T2 = 20 
J1 = 1/5            J2 = 4/5







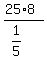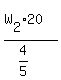
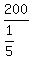To divide by a fraction, invert it and multiply:













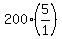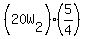
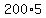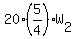
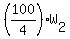
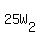
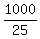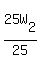
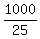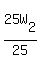 40 = W2 

So it will take a total of 40 workers.  There are already 25 workers,
so it will take 40-25 = 15 more workers.

Answer: 15 more workers.

Edwin