|
Question 622351: a three-digit number satisfies the following conditions: the digits are consecutive whole numbers; the sum of the digits is greater than 10 and less than 20; and the tens digit is an odd number. what is the number?
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! a three-digit number satisfies the following conditions: the digits are consecutive whole numbers; the sum of the digits is greater than 10 and less than 20; and the tens digit is an odd number. what is the number?
Let the smallest digit be S
Then other digits are: S + 1, and S + 2, since all 3 are consecutive integers
Sum of numbers = S + S + 1 + S + 2, or 3S + 3
Since their sum is greater than 10 and less than 20, we can say that:
10 < 3S + 3 < 20
10 – 3 < 3S + 3 – 3 < 20 – 3 --- Subtracting 3 from each section of the compound inequality
7 < 3S < 17
 < S < < S <  --- Dividing each section of the compound inequality by 3 --- Dividing each section of the compound inequality by 3
This means that the SMALLEST digit is greater than  , or , or 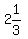 , but less than , but less than  , or , or 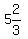
Now, the integers that are greater than 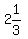 , but less than , but less than 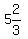 are: 3, 4, and 5 are: 3, 4, and 5
Smallest integer being 3
The smallest integer CANNOT BE 3 because the next consecutive number, or the middle digit, or tens digit, would be 4, which contradicts the given clue that the tens digit is odd
Smallest integer being 4
The smallest integer CAN BE 4 because the next consecutive number, or the middle digit, or tens digit, would be 5, which is true, based on the given clue that the tens digit is odd
Smallest integer being 5
The smallest integer CANNOT BE 5 because the next consecutive number, or the middle digit, or tens digit, would be 6, which contradicts the given clue that the tens digit is odd
Therefore, the 3 digits are: 4, 5, and 6, making the 3-digit number: 
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|
| |