|
Question 442300: A boat traveled 210 miles downstream and back. The trip downstream took 10 hours. The trip back
took 70 hours. What is the speed of the boat in still water? What is the speed of the current?
Found 3 solutions by mananth, ikleyn, timofer:
Answer by mananth(16949)   (Show Source):
You can put this solution on YOUR website! against current x- 70.00 hours
with current x+ 10.00 hours
Distance = same=210
Boat speed =x
current speed =y
t=d/r
210/(x-y)=70.00
70(x-y)=210.00
70x-70y =210 ....................1
210/(x+y)=10.00
10.00(x +y)=210
10.00x+10.00y=210 ...............2
Multiply (1) by 1.00
Multiply (2) by 7.00
we get
70x-70y=210
70x+70y=1470
140x=1680
/140
x =12 mph Boat speed
plug value of x in (1)
70x-70y=210
840-70y=210
-70y=210-840
-70y=-630
y=9 mph current speed
Answer by ikleyn(53472)  (Show Source):
You can put this solution on YOUR website! .
A boat traveled 210 miles downstream and back. The trip downstream took 10 hours. The trip back
took 70 hours. What is the speed of the boat in still water? What is the speed of the current?
~~~~~~~~~~~~~~~~~~~~~~~~~
The solution by @mananth has too much excessive calculations,
which means that his computer code, which produces his text and calculations,
is badly organized and creates anti-pedagigic narrative.
As a result, the solution by @mananth scares readers and is a bad way to teach.
Below is my solution, which is a standard treatment of the problem without making unnecessary calculations.
The effective speed downstream is
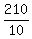 = 21 mph.
The effective speed upstream is
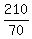 = 3 mph.
If u is the rate of the boat at no current and v is the rate of current, then
u + v = 21 (1)
u - v = 3 (2)
By adding equations, you get 2u = 21 + 3 = 24, u = 24/2 = 12 mph.
Bu subtracting eq.(2) from eq.(1), you get 2v = 21 - 3 = 18, v = 18/2 = 9 mph.
ANSWER. The rate of the boat at no current is 12 mph.
The rate of the current is 9 mph.
Solved in the most straightforward form and in the most educative way, without making excessive calculations.
Answer by timofer(138)  (Show Source):
|
|
|
| |
