|
Question 431642: PROBLEM 1:
A two digit number with 2 different digits has a special property: "When the sum of its digits is added to the product of its digits, the result is the number itself." What is the smallest number with this property?
PROBLEM 2:
Six is a perfect number because its factors ( not including 6)add up to itself. What are all the perfect numbers between 20 and 30?
Found 2 solutions by ankor@dixie-net.com, richard1234:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A two digit number with 2 different digits has a special property:
"When the sum of its digits is added to the product of its digits, the result is the number itself."
What is the smallest number with this property?
:
x = 10's digit
y = units
then
10x+y = the number
:
x + y + xy = 10x + y
xy = 10x - x + y - y
xy = 9x
y = 
y = 9 is the units
then
19 is the smallest number with this property.
:
See if that is true
1 + 9 + (1*9) = 10(1) + 9
:
:
PROBLEM 2:
Six is a perfect number because its factors ( not including 6)add up to itself. What are all the perfect numbers between 20 and 30?
28: 1 + 2 + 4 + 7 + 14
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. Suppose the number is 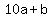 , where , where 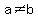 . Then, . Then,  --> -->  --> -->  , b = 9. We can assume , b = 9. We can assume  to be as small as possible, so 19 is the smallest such number. to be as small as possible, so 19 is the smallest such number.
2. 28, because the sum of its proper divisors is 1+2+4+7+14 = 28. In fact, all even perfect numbers are in the form 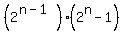 where where  is prime. This is because the sum of divisors function is a multiplicative function for relatively prime integers. When is prime. This is because the sum of divisors function is a multiplicative function for relatively prime integers. When  , ,  , prime, so , prime, so  , a perfect number. , a perfect number.
|
|
|
| |