Question 430328: determine the number oof seven-digit numbers (in base 10) which are divisible by 11 and whose digit sums are 61
if possible please show detailed working out
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! A number is divisible by 11 if and only if
S(even) - S(odd) ≡ 0 (mod 11).
If we let our number be  , then , then  and and 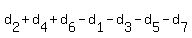 ≡ 0 (mod 11) --> ≡ 0 (mod 11) --> 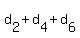 ≡ ≡ 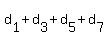 . If we let . If we let  and and  , then k ≡ 61 - k (mod 11) --> 2k ≡ 61 ≡ 6 (mod 11) --> k ≡ 3 (mod 11). , then k ≡ 61 - k (mod 11) --> 2k ≡ 61 ≡ 6 (mod 11) --> k ≡ 3 (mod 11).
This means, 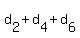 can be equal to 3, 14, 25, 36, 47, or 58. We exclude 3, 14, 36, 47, and 58 because either the even sum or the odd sum becomes too high. Hence, can be equal to 3, 14, 25, 36, 47, or 58. We exclude 3, 14, 36, 47, and 58 because either the even sum or the odd sum becomes too high. Hence,  and and  . .
Fortunately, it is easy to count by hand the number of possible seven-digit numbers. For example, the odd number digits must all be 9's, since 36 is the maximal sum. It is also easy to count the number of ways to obtain 25, since it is not far from 27:
 , ,  , , 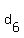 =: =:
9,9,7
9,7,9
7,9,9
8,8,9
8,9,8
9,8,8
The only possible numbers are 9999979, 9997999, 9799999, 9898999, 9899989, and 9998989 (six numbers).
|
|
|