|
Question 345804: What is the formula for the following:
The three least consecutive multiples of 8, the sum of which is greater than 244.
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website! What is the formula for the following:
The three least consecutive multiples of 8, the sum of which is greater than 244.
8n = first multiple of 8
8(n+1) = next multiple of 8
8(n+2) = third multiple of 8
Sum > 244
8n + 8(n+1) + 8(n+2) > 244
8n + 8n + 8 + 8n + 16 > 244
24n + 24 > 244
24n > 220
n > 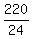 n >
n > 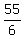 n >
n > 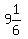 So the smallest possible value n could be is the
smallest integer greater than
So the smallest possible value n could be is the
smallest integer greater than 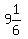 , which is 10.
So
The first multiple of 8 = 8n = 8(10) = 80
The next multiple of 8 = 8(n+1) = 8(11) = 88
The third multiple of 8 = 8(n+2 = 8(12) = 96
Checking: 80+88+96=254, so the sum is greater than 244.
That checks.
Checking to see if they are the least possible such
consecutive multiples of 8. To check this we try
the next lower consecutive multiples of 8. They are
72, 80, 88, but their sum is only 240, so they are too
small, so 80, 88, and 96 are the smallest three consecutive
multiples of 8 whose sum exceeds 244.
Edwin , which is 10.
So
The first multiple of 8 = 8n = 8(10) = 80
The next multiple of 8 = 8(n+1) = 8(11) = 88
The third multiple of 8 = 8(n+2 = 8(12) = 96
Checking: 80+88+96=254, so the sum is greater than 244.
That checks.
Checking to see if they are the least possible such
consecutive multiples of 8. To check this we try
the next lower consecutive multiples of 8. They are
72, 80, 88, but their sum is only 240, so they are too
small, so 80, 88, and 96 are the smallest three consecutive
multiples of 8 whose sum exceeds 244.
Edwin
|
|
|
| |