SOLUTION: What three consecutive numbers have a sum that is 1/5 of their product?

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: What three consecutive numbers have a sum that is 1/5 of their product?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 226398: What three consecutive numbers have a sum that is 1/5 of their product?
Answer by drj(1380) About Me  (Show Source):
You can put this solution on YOUR website!
What three consecutive numbers have a sum that is 1/5 of their product?

Step 1. Let n be one number.

Step 2. Let n%2B1 and n%2B2 be the next two consecutive numbers.

Step 3. Let n%2Bn%2B1%2Bn%2B2=3n%2B3=3%28n%2B1%29 be the sum

Step 4. Let 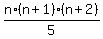n%2A%28n%2B1%29%2A%28n%2B2%29%2F5 be 1%2F5 of their product

Step 5. Then, 3%28n%2B1%29=n%2A%28n%2B1%29%2A%28n%2B2%29%2F5 since the three consecutive numbers have a sum that is 1/5 of their product.

Step 6. Solving equation in Step 5, yields the following steps.

Divide n%2B1 to simplify equation



3=n%2A%28n%2B2%29%2F5

Multiply by 5 to get rid of denominator

3%2A5=n%2A%28n%2B2%29

15=n%5E2%2B2n

Subtract 15 from both sides of the equation

15-15=n%5E2%2B2n-15

0=n%5E2%2B2n-15

Step 7. Factoring the above quadratic equation yields the following

0=n%5E2%2B2n-15=%28n%2B5%29%28n-3%29

Step 8. So n%2B5=0 and n-3=0 or n=-5 and n=3

Step 9. With n=-5, n%2B1=-4 and n%2B2=-3. Check these numbers with the equation in Step 5 3%28n%2B1%29=n%2A%28n%2B1%29%2A%28n%2B2%29%2F5. And

-5-4-3=%28-5%29%2A%28-4%29%2A%28-3%29%2F5

-12=-12 which is a true statement

Step 10. With n=3, n%2B1=4 and n%2B2=5. Check these numbers with the equation in Step 5 3%28n%2B1%29=n%2A%28n%2B1%29%2A%28n%2B2%29%2F5. And

3%2B4%2B5=3%2A4%2A5%2F5

12=12 which is a true statement.

Step 11. ANSWER: There are two sets of consecutive numbers, they are 3, 4, 5 and -5, -4, -3.

I hope the above steps were helpful.

For FREE Step-By-Step videos in Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.

Good luck in your studies!

Respectfully,
Dr J