|
Question 216488: the difference of two whole numbersis 2. if two times the squareof the smaller number added too three times the squareof the larger numbers equal 140, find the numbers
Answer by drj(1380)   (Show Source): (Show Source):
You can put this solution on YOUR website! The difference of two whole numbers is 2. if two times the square of the smaller number added too three times the square of the larger numbers equal 140, find the numbers.
Step 1. Let x be one number and x+2 be the other number.
Step 2. Let 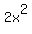 be two times the square of the smaller number. be two times the square of the smaller number.
Step 3. Let 3*(x+2)^2 be three times the square of the larger number.
Step 4. The,  since two times the square of the smaller number added too three times the square of the larger numbers equal 140. since two times the square of the smaller number added too three times the square of the larger numbers equal 140.
Step 5. Solving yields the following steps:




Subtract 140 from both sides of the equation to get a quadratic equation.


Step 6. To solve, we can use the quadratic equation given as

where a=5, b=12, and c=-128
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=2704 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 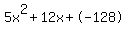 can be factored: can be factored:

Again, the answer is: 4, -6.4.
Here's your graph:
 |
Select the positive number since we want whole numbers gives x=4 and x+2=6
Check... which is a true statement. which is a true statement.
Step 7. ANSWER: The numbers are 4 and 6.
I hope the above steps were helpful.
For FREE Step-By-Step videos in Introduction to Algebra, please visit
http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit
http://www.FreedomUniversity.TV/courses/Trigonometry.
Good luck in your studies!
Respectfully,
Dr J
|
|
|
| |