SOLUTION: Farmer Billy Bob has 210m of fencing to enclose his pig pen on all 4 sides. What dimensions should his pig pen be to enclose the largest possible area?

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: Farmer Billy Bob has 210m of fencing to enclose his pig pen on all 4 sides. What dimensions should his pig pen be to enclose the largest possible area?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 176693: Farmer Billy Bob has 210m of fencing to enclose his pig pen on all 4 sides. What dimensions should his pig pen be to enclose the largest possible area?
Found 2 solutions by Earlsdon, solver91311:
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
Start by writing the formula for the perimeter of a rectangle (assuming, of course, that the pen will be rectangular):
P+=+2%28L%2BW%29 Substitute the given P = 210.
210+=+2%28L%2BW%29
Divide both sides by 2.
105+=+L%2BW and rewite this as:
L+=+105-W
Now the area of a rectangle is given by:
A+=+L%2AW Substitute, from above, L = 105-W.
A+=+%28105-W%29%2AW Simplify.
A+=+105W-W%5E2
Rewrite as:
A+=+-W%5E2%2B105W This is a quadratic equation that represents the area and the maximum point will be at the vertex of the parabola.
This point is given by:
W+=+%28-b%29%2F2a where: a = -1 and b = 105, so...
W+=+%28-105%29%2F2%28-1%29
highlight%28W+=+52.5%29meters. This will be the dimension of the width of the pen.
The length is given (from above) by:
L+=+105-W
L+=+105-52.5
highlight%28L+=+52.5%29meters. This will be the dimension of the length of the pen.
This answer should come as no surprise to you as it is well known that the largest rectangular area enclosed by a given perimeter is in the form of a square.
Check:
P+=+2%28L%2BW%29 Substitute L = 52.5 and W = 52.5
P+=+2%2852.5%2B52.5%29
P+=+2%28105%29
P+=+210meters, the given perimeter.

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
The area of a rectangle is given by the length times the width, and the perimeter is given by 2 times the length plus 2 times the width:

A+=+LW+ and P+=+2L+%2B+2W

We want to maximize A subject to the constraint that P+=+210.


P+=+210 → 2L+%2B+2W+=+210, so solve for either L or W.

2L+=+210+-+2W → L+=+105+-+W

Now substitute this expression for L into the Area function:

A%28W%29+=+W%28105+-+W%29 → A%28W%29+=+-W%5E2+%2B+105W

Now we have a second degree polynomial with a negative lead coefficient, so the graph is a concave down parabola. The vertex of a concave down parabola is a maximum, so we need to find the value of the W coordinate for the vertex. The vertex of a parabola expressed in 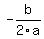f%28x%29+=+ax%5E2+%2B+bx+%2B+c has an x-coordinate of -b%2F2a. In this problem we have a+=+-1 and b+=+105, so the W-coordinate is at W+=+-105%2F%282%28-1%29%29+=+52.5. Hence, for the maximum area, the width must be 52.5 meters.

So if P+=+210 and W+=+52.5, L+=+105+-+52.5+=+52.5 and the pig pen needs to be a square 52.5 meters on each side.

As you may expect, it is true in general that a rectangle with maximum area for a given perimeter is a square. For extra credit, prove it.