|
Question 122616: Please help me solve this equation!
1.) Find two numbers with a sum of 4 and a product of 13.
answer should be [2+3i] and [2-3i]
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let one of the numbers be represented by x and the other one by y
.
You are told that the sum of the two numbers is 4. This can be written in equation form as:
.

.
You are also told that the product of the two numbers is 13. This can be written in equation
form as:
.

.
So you now have two equations, each with the two unknowns and you need to solve them. One way
to get a solution is to use substitution. Solve one of the equations by finding one of the
unknowns in terms of the other and substitute this result into the other equation.
.
Let's begin by solving the product equation for y in terms of x. Divide both sides of the
product equation by x and you get:
.

.
Then in the sum equation you can substitute 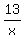 for y and you get: for y and you get:
.

.
Get rid of the denominator by multiplying both sides (all terms) of this equation by x
to get:
.

.
Get this into standard quadratic form by subtracting 4x from both sides to convert the
equation to:
.

.
Solve this by using the quadratic formula. Since this equation is of the standard form:
.

.
by comparing this standard form term-by-term with with the equation for this problem you
can see that a = 1, b = -4, and c = 13. The quadratic formula says that the solution to
a quadratic equation of the standard form is given by:
.

.
So all that you have to do is to substitute your values for a, b, and c into this solution
equation and you have:
.

.
This simplifies to:
.

.
But 
.
and substituting this result into the answer simplifies it to:
.

.
So two possible answers for x are  and and 
.
To find the corresponding values of y, return to the sum equation which said that:
.

.
Substitute  into this equation and you get: into this equation and you get:
.

.
Solve for y by subtracting 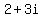 from both sides and you get: from both sides and you get:
.

.
This tells you that if  then then  . .
.
Next, solve for the other possible value of x, namely  . Again, start with . Again, start with
the equation:
.

.
Substitute  into this equation and you get: into this equation and you get:
.

.
Solve for y by subtracting 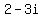 from both sides and you get: from both sides and you get:
.

.
This tells you that if  then then  . .
.
Now examining the two sets of answers you see that if one of the numbers (x or y) is 
then the other number is 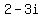 . So in either case, that is the answer. One number is . So in either case, that is the answer. One number is
 and the other number is and the other number is 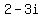 . .
.
Hope this helps you to understand the problem and one way that it can be solved.
.
|
|
|
| |