SOLUTION: Find the sum of the following series: <img src="https://i.ibb.co/b6bHYcd/Code-Cogs-Eqn.gif" height = "35px">

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: Find the sum of the following series: <img src="https://i.ibb.co/b6bHYcd/Code-Cogs-Eqn.gif" height = "35px">       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1205331: Find the sum of the following series:


Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52800) About Me  (Show Source):
You can put this solution on YOUR website!
.
Find the sum of the following series:

~~~~~~~~~~~~~~~~~~~~~ 

Make a standard operation of "rationalizing the denominators" over each separate term/addend


   1%2F%28sqrt%281%29%2Bsqrt%282%29%29 =  = %28sqrt%282%29-sqrt%281%29%29%2F%282-1%29 = sqrt%282%29-sqrt%281%29


   1%2F%28sqrt%282%29%2Bsqrt%283%29%29 =  = %28sqrt%283%29-sqrt%282%29%29%2F%283-2%29 = sqrt%283%29-sqrt%282%29


   1%2F%28sqrt%283%29%2Bsqrt%284%29%29 =  = %28sqrt%284%29-sqrt%283%29%29%2F%284-3%29 = sqrt%284%29-sqrt%283%29


   1%2F%28sqrt%284%29%2Bsqrt%285%29%29 =  = %28sqrt%285%29-sqrt%284%29%29%2F%285-4%29 = sqrt%285%29-sqrt%284%29


    . . .    and so on  . . . 


   1%2F%28sqrt%2835%29%2Bsqrt%2836%29%29 =  = %28sqrt%2836%29-sqrt%2835%29%29%2F%2836-35%29 = sqrt%2836%29-sqrt%2835%29


    +-------------------------------------------------+
    |   Now add all these identities, line by line.   |
    +-------------------------------------------------+


In the right side, all the interior terms with opposite signs will cancel each other.

So, in the right side, you will get the difference  sqrt%2836%29 - sqrt%281%29.

In the left side, you will get the sought sum


     


    = sqrt%2836%29 - sqrt%281%29 = 6 - 1 = 5.


ANSWER.  The given sum is 5.

Solved.

--------------------

To see many other similar and different solved problems, look into these lessons
    - HOW TO rationalize a fraction by making its denominator free of square roots
    - HOW TO rationalize a fraction by making its denominator free of cubic roots
    - Amazing calculations with fractions that contain quadratic irrationalities in denominators
in this site.

Consider them as your textbook,  handbook,  guidebook,  tutorials and/or a  (free of charge)  home teacher.

Learn the subject from there and become an expert.



Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Each term is of the form 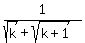1%2F%28sqrt%28k%29%2Bsqrt%28k%2B1%29%29 where k ranges from k = 1 to k = 35.

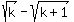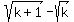Rationalize the denominator, by multiplying top and bottom by sqrt%28k%29-sqrt%28k%2B1%29, and you should get sqrt%28k%2B1%29-sqrt%28k%29 after the simplification is done.
Therefore, 1%2F%28sqrt%28k%29%2Bsqrt%28k%2B1%29%29+=+sqrt%28k%2B1%29-sqrt%28k%29
I'll leave the scratch work for the student to do.

If k = 1, then, sqrt%28k%2B1%29-sqrt%28k%29+=+sqrt%281%2B1%29-sqrt%281%29=+sqrt%282%29-sqrt%281%29
If k = 2, then, sqrt%28k%2B1%29-sqrt%28k%29+=+sqrt%282%2B1%29-sqrt%282%29=+sqrt%283%29-sqrt%282%29
If k = 3, then, sqrt%28k%2B1%29-sqrt%28k%29+=+sqrt%283%2B1%29-sqrt%283%29=+sqrt%284%29-sqrt%283%29
Adding those terms gets us


The inner terms sqrt%282%29 and sqrt%283%29 cancel out.
This will extend to the summation of terms k = 1 through k = 35
The inner terms 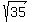sqrt%282%29, sqrt%283%29, ... , sqrt%2834%29, sqrt%2835%29 cancel leaving behind sqrt%2836%29-sqrt%281%29+=+6-1+=+5

For more info and examples, search out "telescoping series".
The name is due to the fact the long series collapses to a very small expression since the inner terms cancel out.
https://mathworld.wolfram.com/TelescopingSum.html

Answer: 5