SOLUTION: the slope of a family of curves at any point (x,y) is equal to (x+1)(x+2). find the equation of the curve that is passing through the point (-3,-3/2).

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: the slope of a family of curves at any point (x,y) is equal to (x+1)(x+2). find the equation of the curve that is passing through the point (-3,-3/2).      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1150483: the slope of a family of curves at any point (x,y) is equal to (x+1)(x+2). find the equation of the curve that is passing through the point (-3,-3/2).
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
Point-Slope Form, y-k=m%28x-h%29

y-%28-3%2F2%29=%28-3%2B1%29%28-3%2F2%2B2%29%28x-%28-3%29%29
Simplify this and put into whichever form you need.

Answer by ikleyn(52906) About Me  (Show Source):
You can put this solution on YOUR website!
.
the slope of a family of curves at any point (x,y) is equal to (x+1)(x+2). find the equation of the curve
that is passing through the point (-3,-3/2).
~~~~~~~~~~~~~~


            The  "solution"  in the post by  @josgarithmetic is  WRONG :   he incorrectly uses formula to calculate the slope.

            I came to bring a correct solution. 


At the given point (-3,-3/2), the slope is  (-3+1)*(-3+2) = (-2)*(-1) = 2.


Therefore, the equation of the straight line at this point is


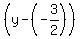    %28y+-+%28-3%2F2%29%29 = 2*(x-(-3)),      (1)  

or

    2y + 3 = 4*(x+3),

    2y + 3 = 4x + 12

    4x - 2y = -9.                (2)


You may choose any of the equations (1) or (2) - they are EQUIVALENT.

Solved.