|
Question 1146051: A crew rowed upstream from A to B and then back to C between A and B. the time from A to B 1hour and from B to C is 12 minutes. the distance from B to C is 1/3 of the distance between A and B. Find the rate of the current if the rate of the crew in still water is 4 miles per hour.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39625)   (Show Source):
Answer by ikleyn(52847)  (Show Source):
You can put this solution on YOUR website! .
Watch attentively my steps.
Let "c" be the rate of current, in miles.
Then the rate moving upstream is (4-c) miles per hour,
while the rate moving downstream is (4+c) miles per hour.
Let d(A,B) be the distance from A to B, and let d(B,C) is the distance from B to C.
Since the travel upstream from A to B took 1 hour, the distance
d(A,B) = the rate moving upstream * 1 hour = (4-c)*1 = 4-c miles.
Since the travel downstream from B to C took 12 minutes =  of an hour, the distance
d(B,C)) = the rate moving downstream * hour = 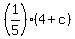 miles.
From the condition, you are given that d(B,C) =  .d(A,C).
It gives you an equation
.(4 + c) = .(4 - c).
It is your basic equation. The setup is just completed.
To solve the equation, multiply both sides by 15. You will get
3*(4 + c) = 5*(4 - c)
12 + 3c = 20 - 5c
3c + 5c = 20 - 12
8c = 8
c = 1 mile per hour.
ANSWER. The rate of the current is 1 mile per hour.
Solved.
|
|
|
| |
