|
Question 1129602: The product of all the positive divisors of a positive integer N is 6*16*36*96. What is N?
Found 3 solutions by t0hierry, ikleyn, Edwin McCravy:
Answer by t0hierry(194)   (Show Source): (Show Source):
You can put this solution on YOUR website! Write n as
6*16*36*96 and again as
96*36*16*6
now
6*96 = 576
16*36= 576
SO
n^2 = 576^4 = 576^(number of divisors, which is 4) and thus
n = 576^2 = 331776
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solution 1
The product of all positive divisors of a positive integer N is 6*16*36*96 = 331776. (given)
The product of all the positive divisors of the number 24 is 2*3*4*6*8*12*24 = 331776.
ANSWER. The number under the question is 24.
Solved.
It is "experimental", or "empiric" prove.
The solution can be made with logical reasoning, too.
Solution 2
Notice that 6*16*36*96 =  . (*)
So, it is prime decomposition into the product of prime numbers 2 and 3 with their corresponding degrees.
It implies that the "base" number N is the product of prime numbers 2 and 3 in some degrees : N = . (*)
So, it is prime decomposition into the product of prime numbers 2 and 3 with their corresponding degrees.
It implies that the "base" number N is the product of prime numbers 2 and 3 in some degrees : N = 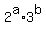 . (**)
From the other side, if R is some positive integer divisor of N, then S= N/R is its other positive integer divisor -
- therefore, the product of all divisors of the integer N is N in some degree - namely in the degree, equal to half
of the number of all its divisors.
Thus the number (*) is some degree of N, and looking into formula (**), you may hypothesize than the degree b is 4.
Then . (**)
From the other side, if R is some positive integer divisor of N, then S= N/R is its other positive integer divisor -
- therefore, the product of all divisors of the integer N is N in some degree - namely in the degree, equal to half
of the number of all its divisors.
Thus the number (*) is some degree of N, and looking into formula (**), you may hypothesize than the degree b is 4.
Then  must be the 4-th degree, and then it necessary is must be the 4-th degree, and then it necessary is 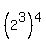 , so the number N is necessary N = , so the number N is necessary N = 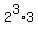 = 8*3 = 24,
exactly as we found it in the first, "experimental", or "empiric" proof.
Notice that = 8*3 = 24,
exactly as we found it in the first, "experimental", or "empiric" proof.
Notice that  = =  and that the number 24 has 8 divisors 1, 2, 3, 4, 6, 8, 12 and 24. and that the number 24 has 8 divisors 1, 2, 3, 4, 6, 8, 12 and 24.
Solved twice and explained.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! The product of all the positive divisors of a positive integer N is 6∙16∙36∙96. What is N?
We prime factor those factors:
6 = 2∙3
16 = 2∙2∙2∙2
36 = 2∙2∙3∙3
96 = 2∙2∙2∙2∙2∙3
Therefore 6∙16∙36∙96 = 21234
From above we see that N contains prime factors 2 and 3 and ONLY those two
prime factors. Now we must determine how many times N contains each as a
factor.
N cannot contain the factor 3 more than once. Because: If so, N would
contain 2∙3∙3 as a factor. Then the factors of N would contain factors
1, 2, 3, 2∙3, 3∙3, 2∙3∙3, which would produce a product of factors 23∙36.
Then the product of factors of N would contain 3 as a factor 6 times.
However we know that the product of factors of N contains 3 as a factor only
4 times.
Therefore N contains 3 as a factor exactly once, no more and no less!
So we only need determine how many times N contains 2 as a factor.
It must contain 2 as a factor more than once, for if N contained 2 as a
factor only once, then N would be 2∙3=6, with product of factors
(1)(2)(3)(2∙3) = 22∙33, not 21234.
N also must contain 2 as a factor more than twice, for if it contained 2 as
a factor only twice, then N would be 2∙2∙3=12, with product of factors
(1)(2)(3)(2∙2)(2∙3)(2∙2∙3) = 26∙33, not 21234.
So we try N as containing 2 as a factor 3 times. That would make N = 2∙2∙3
= 24. Then the product of factors of N would be
(2)(3)(2∙2)(2∙3)(2∙2∙2)(2∙2∙3)(2∙2∙2∙3) = 21234, which
is exactly what we're looking for!
So the answer is N = 24.
Edwin
|
|
|
| |