Question 1113620: Suppose the product of n consecutive, positive four-digit integers is divisible by 2015^2 . What is the least possible value of n ?
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! Ans:  is the least number. is the least number.
——————————
The workout:
You start with 2015 and multiply by 2016, 2017, … , 2046
N = 2015*2016*…*2046 will be divisible by 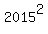
—
Why?
Because 2015 = 5*13*31 —> 5|2015, 13|2015, and 31|2015 (a|b means "a divides b"). With that as the starting point you have one factor of 5, 13, and 31 to start and must multiply by consecutive integers until you have accumulated one additional factor each of 5, 13, and 31. The next number that 31 divides sets the minimum range, and that is (2015+31 = 2046). In all, that is 2046-2015+1 = 32 numbers.
|
|
|