Question 1081867: sum of the digits of a two digits number is 9.when we interchange the digits, it is found that the resulting new number is greater than the original number by 27. what is the two digit number?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The quick answer: 36 and 63.
The fact that the digits add to 9 tells you both numbers are multiples of 9.
Multiples of 9 lesser than 99 are
09,18,27,36,45,54,63,72,81,90.
They come in pairs of one number and its reversed-digits twin.
Obviously, the ones in the middle of the list, 45 and 54, differ by 9.
The next pair, 36 and 63, has as difference of  .
The one after that differs by  , and so on
The show your work way:
If you have to show work, it is shorter to write equations than to explain reasoning in words.
From what I write below, feel free to skip anything that your teacher would not require.
 = the tens digit
 = the ones digit,
with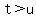 
 (because the sum of digits is 9)
 (because the value of the greater number is 10t+u, and the value of the other, reversed-digits number is 10u+t).
Simplifying,
Then,  ---> 
|
|
|
