SOLUTION: 149. Find 3 consecutive even numbers such that the sum of the 1st and the 3rd numbers exceeds the 2nd number by 10

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: 149. Find 3 consecutive even numbers such that the sum of the 1st and the 3rd numbers exceeds the 2nd number by 10      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1035849: 149. Find 3 consecutive even numbers such that the sum of the 1st and the 3rd numbers exceeds the 2nd number by 10
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
highlight%288%29 , highlight%2810%29 , and highlight%2812%29 .

THE FIFTH GRADER SOLUTION:
No calculation needed.
Three consecutive integers form an arithmetic sequence,
and in an arithmetic sequence the median is the average.
In other words, the middle number is the average of the other two numbers,
which means that the sum of the first and third numbers is 2 times the middle number,
which is the middle number plus the middle number.
The sum exceeds the second (middle) by the value of the middle number,
and the problem says that value is highlight%2810%29 .

MAKING IT LOOK LIKE ALGEBRA:
Let's call the three consecutive even numbers (the first, second, and third even numbers)
x-2 , x , and x%2B2 .
The sum of the first and third numbers is %28x-2%29%2B%28x%2B2%29=2x .
The problem says that sum exceeds the second number by 10 ,
meaning that the is equal to the sum of the first and third numbers is 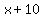x%2B10 .
Our equation is
2x=x%2B10--->2x-x=x%2B10-x--->highlight%28x=10%29 .
So, x-2=10-2=highlight%288%29 , and x%2B2=10%2B2=highlight%2812%29 .

NOTE:
You can always call three consecutive even numbers,
or three consecutive odd numbers x-2 , x , and x%2B2 .
If the x you find at the end is not an odd or even integer as you expected,
the problem has no solution
(or you made a mistake in your calculations).