Question 997311: A milkman ordered his assistant to first remove 3 liters out og he 8 liters of a solution of milk and water and then add 3 liters of water to it.Thinking that it would not make any difference , the lab assistant first added 3 liters of water and then removed 3 liters of the solution. Find the ratio of the expected concentration of the milk to actual concentration of the milk?
1)1:1 2)21:52 3)55:64 4)605:512 5)5:11
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! FOLLOWING INSTRUCTIONS:
Removing  liters from liters from  liters leaves liters leaves  liters. liters.
If the solution water content was  liters if water per liter of original solution, liters if water per liter of original solution,
those  liters of solution now contain liters of solution now contain
 liters of water, and liters of water, and  liters of milk. liters of milk.
Adding  liters of water, you end up with a total of liters of water, you end up with a total of
 liters of new, diluted solution, containing liters of new, diluted solution, containing
 liters of milk. liters of milk.
The expected milk concentration (as a volume/volume fraction) is
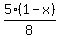
THE WAY THE ASSISTANT DID IT:
If the solution water content was  liters if water per liter of original solution, liters if water per liter of original solution,
in the  liters of original milk solution there was initially liters of original milk solution there was initially
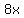 liters of water, and liters of water, and  liters of the milk. liters of the milk.
After adding  liters of water, the resulting solution had a volume of liters of water, the resulting solution had a volume of
 liters of waters, containing liters of waters, containing  liters of the milk. liters of the milk.
The resulting milk concentration (as a volume/volume fraction) is
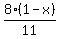 , and does not change on removing , and does not change on removing  liters of solution. liters of solution.
The ratio of expected concentration of the milk to actual concentration of the milk is
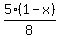 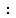 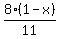 = =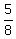 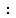  = =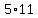   = =   . .
|
|
|