Question 985473: Let P(x)=x^3-2x^2-13x-10
a.determine whether x-5 is a factor if P(x).
b.find another factor of P(x).
c.find a complete factorization of P(x).
d. Solve the equation P(x)=0.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a. To determine whether x-5 is a factor of P(x), calculate P(5), i.e. simply substitute the value of 5 into the polynomial. You will get
P(5) = 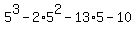 = 125 - 50 - 65 - 10 = 0. = 125 - 50 - 65 - 10 = 0.
According wi the Remainder Theorem (see, for example, the lesson Divisibility of polynomial f(x) by binomial x-a in this site), the binom x-5 is a factor of the polynomial P(x).
b. Make the long division of the polynomial P(x) = 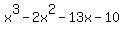 by by 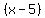 . You will get . You will get
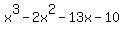 = = 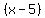 . .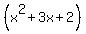 . .
So, the polynomial 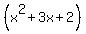 is another factor of the polynomial P(x). is another factor of the polynomial P(x).
c. The quadratic polynomial 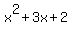 has the roots has the roots  = -1 and = -1 and  = -2 (use the quadratic formula Introduction into Quadratic Equations or the Vieta's theorem Solving quadratic equations without quadratic formula, lessons in this site) = -2 (use the quadratic formula Introduction into Quadratic Equations or the Vieta's theorem Solving quadratic equations without quadratic formula, lessons in this site)
It implies that 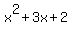 = = 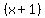 . . . .
Therefore,
P(x) = 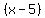 . .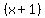 . .
is the complete factorization of the polynomial P(x) = 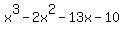 . .
d. Since P(x) = 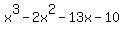 = = 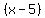 . .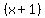 . . , the roots of the polynomial , the roots of the polynomial 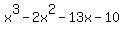 are 5, -1 and -2. are 5, -1 and -2.
The solution is completed.
|
|
|