Word problem into a rational equation, 18 lbs of fruit purchased, there where $9
worth of apples and $2.40 of bananas, price per lb of apples is three times more
than price per lb of bananas. How many lbs of apples and how many lbs of bananas
where purchased? How do I solve?
My email is cyclo29@yahoo.com thank you!
Let the number of pounds of apples = x.
>>18 lbs of fruit purchased<<
So the number of pounds of bananas = 18-x
price per lb of apples is three times more than price per lb of bananas.
Let the price per pound of bananas = y
Then the price per pound of apples = 3y.
>>...there where $9 worth of apples...<<


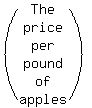

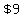 Therefore:
(x)(3y) = 9
3xy = 9
xy = 3
Therefore:
(x)(3y) = 9
3xy = 9
xy = 3
>>...and $2.40 of bananas,...<<


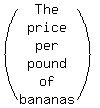

 Therefore:
(18-x)(y) = 2.40
y(18-x) = 2.40
18y-xy = 2.40
So we have the two equations:
Therefore:
(18-x)(y) = 2.40
y(18-x) = 2.40
18y-xy = 2.40
So we have the two equations:
 Substitute 3 for xy in the second equation:
18y-xy = 2.40
18y-3 = 2.40
18y = 5.40
y = 0.30,
[so bananas sold for 30 cents a pound, and apples 90 cents a pound.]
Substitute y = 0.30 in the first equation:
xy = 3
x(0.30) = 3
x =
Substitute 3 for xy in the second equation:
18y-xy = 2.40
18y-3 = 2.40
18y = 5.40
y = 0.30,
[so bananas sold for 30 cents a pound, and apples 90 cents a pound.]
Substitute y = 0.30 in the first equation:
xy = 3
x(0.30) = 3
x = 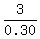 x = 10
So there were 10 pounds of apples purchased.
And therefore there were 18-x or 18-10 or 8 pounds of bananas.
Edwin
x = 10
So there were 10 pounds of apples purchased.
And therefore there were 18-x or 18-10 or 8 pounds of bananas.
Edwin