Question 960751: The radiator of a truck contains 12 gallons of water. We draw off 3 gallons and replace it by alcohol, then draw off 3 gallons of the mixture and replace it by alcohol,etc., until 8 drawings and replacement have been made. How much alcohol is in the final mixture?
Found 4 solutions by josgarithmetic, BustaKnuckle, greenestamps, ikleyn:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by BustaKnuckle(1)   (Show Source): (Show Source):
You can put this solution on YOUR website! First of all, that reply is not an answer lol.
Ok, so to the solution. We know it is a geometric sequence so we need to find the ratio and the first term in order to find the sum.
Finding the first term is easy, if we take away 3 gallons of water and replace it with 3 gallons of alcohol then there are 9 gallons of water and 3 gallons of alcohol. So our first term is 3.
Finding the ratio is a bit more tricky. We need to find the second term. We know that 1/4 of the solution is alcohol so if we take out 3 gallons of the solution and 1/3 of 3 is 1 then we take out 1 gallon of alcohol then we add back in 3 gallon we know 2+3 is 5 so now there are 5 gallons of alcohol and 7 gallons of water. Now we know the ratio is 5/3.
Now we can plug it into the formula.  . I'm not gonna show all the steps but you should get the answer. . I'm not gonna show all the steps but you should get the answer.
Note: I'm not entirely sure on the=is answer as I was having trouble on this problem as well :P
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The analysis by the other tutor is faulty....
And if you evaluate the expression he shows for the amount of alcohol after the 8 drawings and replacements, it is more than 12 gallons -- which of course is nonsense.
I did some ugly calculations for the first few drawings and replacements and noticed a clear pattern in the results; then I verified my calculations using an excel spreadsheet.
Then I finally saw the simple explanation of the pattern I saw, and thus an easy path to the answer to the problem.
Each time a drawing and replacement is made, 1/4 of the mixture is taken out and replaced with pure alcohol. That means that with each drawing and replacement, the amount of water remaining gets reduced by a factor of 3/4.
So after 8 drawings and replacements, the amount of water remaining is
 = 1.201355 gallons, to far more decimal places than practical. = 1.201355 gallons, to far more decimal places than practical.
So the amount of alcohol in the radiator at that time is
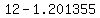 = 10.798645 gallons = 10.798645 gallons
Answer by ikleyn(52781)   (Show Source): (Show Source):
|
|
|