Question 921457: 1. A piece of rope was cut into 2 parts such that the lengths of the two are in the ratio 5:6. If one piece was longer by 110 m, how long was each piece?
A.L=30,W=40 m
B.L=90,W=100 m
C.L=80,W=90 m
D.L=70,W=80 m
E.L=50,W=60 m
2. Half of the class scored 90 in the test. One-third of the class scored 89. What is the average grade of the entire class?
A.88 1/2
B.88 5/6
C.88 2/3
D.88 4/5
E.88
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your problems must have typos, because they make no sense as written.
Otherwise, the person who invented those problems makes no sense.
If you have to make sense of nonsense, the intended answer must have been
E L=50,W=60 m, for problem 1, and there is no answer possible for problem 2.
1. A piece of rope was cut into 2 parts such that the lengths of the two are in the ratio 5:6.
If one piece was longer than the other by 110 m, the lonfger piece should be longer than 110 m, and none of the answers are correct.
A better problem would state that the original length of rope was 110 m, the answer would be E.
In any case, of all the answer options given, the only one with lengths in a ratio of 5:6 is E.
2. Half of the class scored 90 in the test. One-third of the class scored 89. There is no explanation about what happened to the rest of the class (one-sixth of the class). Without the missing information, one guess is as good as another.
 , so what happened to the other , so what happened to the other  of the class? of the class?
Were they absent on the day of the exam, so the average is calculated only for the students who took the exam? If it were so, the average would have been between 89 and 90.
If they took the exam, what average score did they get? Without information about their scores, we cannot calculate the average for the whole class.
If their average score had been  , the average score of all 6 sixths of the class would be , the average score of all 6 sixths of the class would be
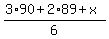 , because , because
 of the class averaged 90, of the class averaged 90,
 of the class averaged 89, of the class averaged 89,
and the remaining  of the class averaged of the class averaged  . .
Then, that average would have been

 <---> <---> <---> <--->
That tells us that
If the answer was supposed to be A.88 1/2, the other one-sixth must have an average score of 83.
If the answer was supposed to be B.88 5/6, the other one-sixth must have an average score of 85.
If the answer was supposed to be C.88 2/3, the other one-sixth must have an average score of 84.
If the answer was supposed to be D.88 4/5, the other one-sixth must have an average score of 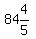 . .
If the answer was supposed to be E.88, the other one-sixth must have an average score of 80.
All those outcomes are possible and likely, so there is no way to make sense of the problem.
|
|
|