Jenna needs 100 liters if a 15% alcohol solution. If she has a 12% alcohol solution and a 20% alcohol solution available, how many of each should sheix to get the desired solution?
Let amount of 12% solution to be mixed be T
Then amount of 20% solution to be mixed = 100 – T
Therefore, we have: .12(T) + .2(100 – T) = .15(100)
.12T + 20 - .2T = 15
.12T - .2T = 15 – 20
- .08T = - 5
T, or amount of 12% solution to be mixed = 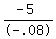 , or
, or 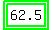 L
L
Amount of 20% solution to be mixed = 100 – 62.5, or 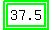 L
L