Question 890580: Two alloys A and B are composed of two basic elements. The ratios of the components of the two basic elements in the two alloys are 5:3 and 1:2 respectively. A new alloy X is formed by mixing the two alloys A and B in the ratio 4:3.What is the ratio of the compositions of the two basic elements in alloy X.
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Ratio of the two elements as x:y, assuming based on masses.
Let p = how much of alloy A
Let v = how much of alloy B
Concentration of x in alloy A,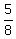 
Concentration of y in alloy A, 
Concentration of x in alloy B, 
Concentration of y in alloy B, 
THE MIXTURE TO PREPARE
Concentration of x in mixture, 
Concentration of y in mixture,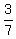 
Account for material x: 
Account for material y: 
The "account" equations are a system of two linear equations in two unknowns. Solve any way you like or know.---------- or, continuing,
Lowest common denominator of those two equations is 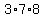 . Multiplying all members by LCD and simplifying, and solving the two equations will give:
 AND  .
The complete solution is still not finished but this is a long way done for finding the answer to the question,"ratio of the two basic elements in the alloy X". Knowing p and v, you only know how much of the two alloys to use.
---
Actually, you already know the ratio of the two basic elements because they were given in the problem description. The best question, now answered, was HOW MUCH OF ALLOY A AND ALLOY B to use. This ratio is 40 parts of A to 9 parts of B.
|
|
|
