Question 840843: two men A and B CAN PAINT A HOUSE IN 18 DAYS.THEY WORK TOGETHER IN 8 DAYS AND THEN B GOES AWAY AND A ALONE FINISHES THE WORK IN 15 DAYS.HOW LONG WOULD EACH OF THEM TAKE TO FINISH THE WORK SEPERATELY?SIR PLS GIVE ME ITS ALL STEPS(DIRECT AND INDIRECT VARIATION)
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is probably not a mixture problem, but is certainly a uniform rates problem.
One job is "paint the house".
R*t=j uses R for rate in jobs per day, t is time in numbers of days, j is how many jobs. The individual rates for A and B are unknown.
Form their rates as 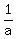 for A and for A and  for B. Again, the unit is jobs per day. for B. Again, the unit is jobs per day.
EXAMINE THE DESCRIPTION
A and B do the job together in 18 days.
 . .
I simply translate the next part of the description into symbols without explaining:

Think very carefully how that makes sense before you continue reading the solution.
...
Your question does not seem fully correct. You might really be wanting just to know the rate separately of each of A and of B. You can solve for these two work rates. The longer translated description contains only "a" as the variable, so you can use that equation to solve for "a", and you then easily have the rate for A, the quantity 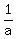 . .
You would then use the combined rates equation, solve it for "b", and use the value found for "a" and compute the value "b".
From this: 





 -------A can do the job alone in 27 days. -------A can do the job alone in 27 days.
Combined Rates Equation, to solve for b:


 , multiplied both sides by 18a; , multiplied both sides by 18a;


-
Substitute for a=27,



 ------------B can do the job alone in 54 days. ------------B can do the job alone in 54 days.
|
|
|