Question 796826: Carbon Dating: The amount of carbon 14 remaining in a sample that originally contained A grams is given by: C(t)=A(0.99879)^t where t is time in years. if tests on a fossilized skull reveal that 99.95% of the carbon 14 has decayed, how old, to the nearest 1,000 years, is the skull?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Carbon Dating: The amount of carbon 14 remaining in a sample that originally contained A grams is given by: C(t)=A(0.99879)^t where t is time in years. if tests on a fossilized skull reveal that 99.95% of the carbon 14 has decayed, how old, to the nearest 1,000 years, is the skull?
:
let A = 1 and C(t) = 1-.9995 = .0005
therefore:
1(.99879)^t = .0005
using nat logs
t*ln(.99879) = ln(.0005)
t = 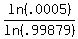
t = 6,277.9 ~ 6000 yrs, however this does not seem right since the half-life of Carbon 14 is 5730 yrs, using a radiation decay calc, I got 62,800 yrs for this amt of decay.
Are you sure this formula is correct?
|
|
|