Question 729873: Hi I am trying to do some word problems by using a system of equations, for example using x and y that way when I set up the two equations I can use either the subsitution method or elimination method. Here are my word problems hope you can help. (:
1. A total of $12,000 is invested, part at 6% simmple interest and part at 3%. If the annual return from the two investments is the same, how much is invested at each rate?
2. A car travels 225 kilometers in the same time that a truck travels 195 kilometers. If the speed of the car is 10 kilometers per hour faster than the speed of the truck, find the speed of each vehicle.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. A total of $12,000 is invested, part at 6% simple interest and part at 3%.
If the annual return from the two investments is the same, how much is invested at each rate?
let x = amt invested at 6%
let y = amt invested at 3%
Two equations
x + y = 12000
and
.06x = .03y
divide both sides by .03, results
2x = y
replace y with 2x in the 1st equation
x + 2x = 12000
3x = 12000
x = 12000/3
x = 4000
I'll let you find y, check the solutions in the interest equation
:
:
2. A car travels 225 kilometers in the same time that a truck travels 195 kilometers.
let x = car speed, let y = truck speed
write a time equation; time = dist/speed
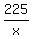 = = 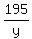
Cross multiply
225y = 195x
divide both sides by 5, results:
45y = 39x
:
" If the speed of the car is 10 kilometers per hour faster than the speed of the truck,"
x - y = 10
x = y + 10
"find the speed of each vehicle."
replace x with (y+10) in the 1st simplified equation
45y = 39(y+10)
45y = 39y + 390
45y - 39y = 390
6y = 390
y = 390/6
y = 65 mph, the speed of the truck
I'll let you find the speed of the car, check your solutions in both equations
|
|
|