Question 581857: please help, this stuff makes no sense to me.
How many liters each of a 12% acid solution and a 20% acid solution should be mixed in order to obtain 4 liters of a 15 % acid solution?
Found 2 solutions by josmiceli, KMST:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's define some variables
Let x be the volume of 12% solution used, in liters.
Let y be the volume of 20% solution used, in liters. (see note below if you have not learned about systems of equations)
The first equation you can set up is
 , based on accounting for volume. , based on accounting for volume.
The amount of acid in a solution, the concentration of the acid and the volume of the solution are related by
 <--> <--> 
You do not need to worry about units as long as they match. That means that if all the volumes are in liters, and all the concentrations are in the same unit, all the amounts will be in the same units, whatever those units are.
To account for the amount of acid, you state that the contributions from the two solutions mixed add up to the amount of acid in the final mix:
 --> --> 
or maybe
 --> --> 
or dividing both sides by 4 
WITH SYSTEM OF EQUATIONS

which you could solve by various methods.
Solving by substitution:
 --> --> 
Then substituting the expression found for y in the other equation,
 --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  or or  is the amount of 12% solution needed. is the amount of 12% solution needed.
So the amount of 20% solution needed is  --> --> 
NOTE (If you are not up to systems of equations)
Then, the amount , in liters of of 20% solution used is 4-x (no need to involve y in this).
The amount of acid contributed by x L of 12 % solution is 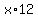 % and the amount contributed by (4-x) L of 20% solution is % and the amount contributed by (4-x) L of 20% solution is 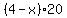 %. They must add up to the amount of acid in 4 L of 15% solution, which is %. They must add up to the amount of acid in 4 L of 15% solution, which is 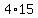 %, so %, so
 --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  or or 
So the amount of 12% solution to be used is  , and the amount of 20% solution to be used is , and the amount of 20% solution to be used is 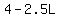 = = . .
|
|
|