Question 578546: Pls. help me solve this math word problem: How many quarts of water must be added to 5 gallons of a 95% solution of ammonia to make an 80% solution? thanks a lot!
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Units are mixed, so let's convert.
1 gallon = 4 quarts, so we start with 20 quarts (5 gallons) of 95% solution.
AS A DILUTION PROBLEM
You may have been told that dilution problems, where you dilute a solution of a substance with just solvent (without any more of that substance), can be solved by applying
 , where V and C are volume and concentration and the subscripts i and f stand for initial and final.
In that case, you would substitute your data, and entering volumes and concentrations in the same units. Let's enter volumes in quarts and concentration in percent
 -->  --> 
So the final volume must be 23.75 quarts and you need to add 23.75-20=3.75 quarts of water.
AS A MIXTURE PROBLEM
Mixture problems can be more complicate involving mixing two (or even more) items with different concentrations of one (or even more) substance(s) of interest. Solving mixture problems require accounting for total mixture amount, and accounting for amount of each substance of interest. You have to balance your books, so to speak. Theoretically, you would end with a system of linear equations. However, the systems are often so simple that you just see one equation. You may solve for the "second" variable in the easy equation without even realizing, so you may not even see a second variable, or a system being solved by substitution. (I will show you that y variable briefly, but we do not need it in this case).
I'll show you the general procedure for solving this kind of problem although this case is very simple.
Total mixture amount:
We add x quarts of water for a total volume of y=x+20 quarts.
We could say that amount of ammonia in the 20 quarts of 95% solution is
 quarts (assuming that the 95% was a volume in volume concentration).
The final amount will have a contribution from both of the liquids being mixed, including the x quarts of water added that had 0% ammonia and added  quarts of ammonia.
The total ammonia in the mixture would be the sum of the two contributions from the 95% solution and from the water:
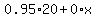
That must be the same as 80% of the y=20+x quarts of final solution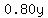, or
 or 
So the final equation would be
 -->  -->  -->  -->  --->  quarts
The system of equations, if we wanted to see it, would be
|
|
|
