SOLUTION: It takes Jimmy 20 minutes to do the dishes. Susie can do the same work in 15 minutes. How long would it take them to do the dishes if they work together?

The other tutor's work is in error. He should have multiplied through
by 60 not 30.

First let's do it in our head!  Then we'll do it by algebra:

The LCM of 20 minutes and 15 minutes is 60 minutes, so:

In 60 minutes Jimmy could do 3 sets of dishes and Susie could do 4 sets of
dishes.  So together they could do 7 sets of dishes in 60 minutes, so it would
only take them 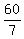 or 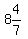 minutes to do 1 set of dishes working together.

But your teacher doesn't want you to do it that way.  They want you to use
algebra.  So we'll now do that.

Make this chart, putting 1 for the number of sets of dishes to be done.
Put in their individual given times, putting x for their time together,
which is what is to be found. Then we find the rates by dividing the
number of sets by the time. 

       Number of sets of dishes done|Time in minutes|Rate in sets of dishes/minute                       
Jimmy               1               |      20       |         1/20
Susie               1               |      15       |         1/15
Together            1               |       x       |         1/x

Form the equation from the rats:

The sum of the individual rates = their combined rats:

                

Multiply through by LCD = 60x 

                

                

                minutes.

Edwin