SOLUTION: What two numbers added together equals negative 10, but when the same two numbers are multiplied together equals negative 20?

Solve the first for y




Substitute 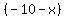 for  in






Multiply through by 



That doesn't factor so we use the quadratic formula:


 





 





Make two fractions





Two solutions for x

 and 

Substituting the first in









so one solkution is

, 

----------------------------

Substituting the second in









so the other solution is

, 

But there are really only two numbers, it's just a 
matter of which you call x and which you call y,
or which you call "the first numner" and
which you call "the second number".

Edwin